特征工程
1,特征和目标的相关性观察
参考:feature/01_columns_info.txt,02_column_corr.txt,03_all_data_corr.txt
2,特征处理批次
第一批,处理方式,异常值收边,分区转换
V0 0.873212 0.866709 0.589606
V1 0.871846 0.832457 0.529013
V8 0.831904 0.799280 0.487379
V27 0.812585 0.765133 0.431041
V31 0.750297 0.749034 0.428427
第二批,
V2 0.638878 0.630160 0.332839
V4 0.603984 0.574775 0.276028
V12 0.594189 0.542429 0.256378
V37 -0.565795 -0.497162 0.253475
V16 0.536748 0.510025 0.239708
V3 0.512074 0.501114 0.221762
第三批,特征掐头去尾
V10 0.394767 0.371067 0.195347
V20 0.444965 0.420424 0.180910
V36 0.319309 0.287696 0.167771
V24 -0.264815 -0.296056 0.162487
V25 -0.019373 0.049352 0.161249
V5 -0.314676 -0.345683 0.158044
V29 0.123329 0.198244 0.146577
V15 0.154020 0.213490 0.146141
V6 0.370037 0.264778 0.144643
V7 0.287815 0.164981 0.143749
V11 -0.263988 -0.293261 0.134465
V23 0.226331 0.043597 0.127452
V18 0.170721 0.162710 0.124676
V9 0.139704 -0.054385 0.124243
V19 -0.114976 -0.171120 0.120048
V28 0.100080 0.081030 0.119935
‘V10,’V20’,’V36’,’V24’,’V25’,’V5’,’V29’,’V15’,’V6’,’V7’,’V11’,’V23’,’V18’,’V9’,’V19’,’V28’
3,特征处理01_PCA消除共线性(及去除异常点)
参考:06_特征处理01_PCA消除共线性.txt
高相关性数据:
print(FeatureTools.get_high_corr_pair(train_data[feature_columns], 0.85))
[(‘V0’, ‘V1’, 0.909), (‘V1’, ‘V8’, 0.875), (‘V4’, ‘V12’, 0.928), (‘V5’, ‘V11’, 0.864), (‘V6’, ‘V7’, 0.918),
(‘V8’, ‘V27’, 0.901), (‘V8’, ‘V31’, 0.878), (‘V10’, ‘V36’, 0.922), (‘V15’, ‘V29’, 0.951)]
print(FeatureTools.get_high_corr_pair(train_data[feature_columns], 0.80))
[(‘V0’, ‘V1’, 0.909), (‘V1’, ‘V8’, 0.875), (‘V1’, ‘V27’, 0.824), (‘V4’, ‘V12’, 0.928), (‘V5’, ‘V11’, 0.864),
(‘V6’, ‘V7’, 0.918), (‘V6’, ‘V16’, 0.847), (‘V8’, ‘V27’, 0.901), (‘V8’, ‘V31’, 0.878), (‘V10’, ‘V36’, 0.922),
(‘V15’, ‘V29’, 0.951)]
使用:0.80
分组:[‘V0’,’V1’,’V8’,’V27’,’V31’],[‘V4’,’V12’],[‘V5’,’V11’],[‘V6’,’V7’,’V16’],[‘V10’,’V36’],[‘V15’,’V29’]
对分组数据使用pca
结论:
[‘V0’,’V1’,’V8’,’V27’,’V31’]:pca阈值0.95,0.97,0.99,效果均变差,故不使用pca处理
[‘V4’,’V12’]:pca阈值0.95,0.98,效果不明显,不使用pca
[‘V6’,’V7’,’V16’]:pca阈值0.95,0.97.0.99,使用0.95pca
[‘V5’,’V11’]:不用
[‘V10’,‘V36’]:使用0.98pca
[’V15‘,’V29‘]:不用
需使用pca处理的:
[‘V6’,’V7’,’V16’]:0.95
[‘V10’,‘V36’]:0.98
自比对:[‘V6’,’V7’,’V16’,’V10’,’V36’],[‘V6_pca’,’V7_pca’,’V10_pca’,’V36_pca’],提升2%,
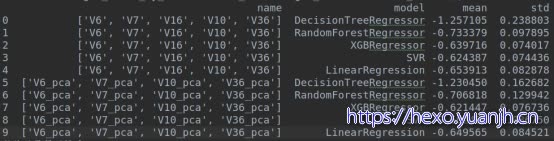
结合特征:[‘V0’, ‘V1’, ‘V8’, ‘V27’, ‘V31’],整体效果提升0.2%(svr微降低)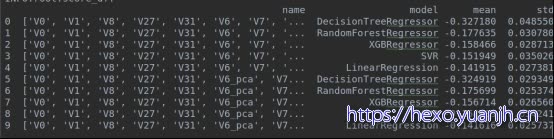
补充:V0,V1的pca处理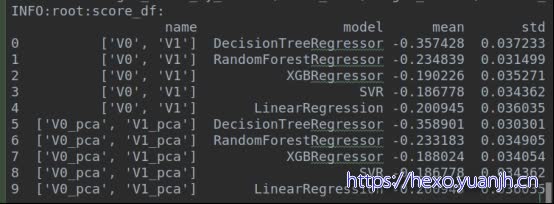
4,特征处理02_L1L2消除共线性和重要性筛选
参考:07_特征处理02_L1L2消除共线性和重要性筛选.txt
依次消除lasso参数abs==0,<0.005,<0.01的特征
最终结论:消除0.005特征,也就是[‘V32’, ‘V34’, ‘V13’, ‘V31’, ‘V15’, ‘V21’]
最优结果:
加入L2根据重要性筛选:
最终结果
L1(abs)阈值0.000001(就是0)删除[‘V31’ ‘V15’ ‘V21’]
L2(abs)阈值0.010,删除:[‘V32’ ‘V13’ ‘V34’]
最终结果(理论上和上面完全相同,当做偶然误差吧)
5,特征处理03_结合01pca和02的L1L2
参考:08_特征处理03_结合01pca和02的L1L2.txt
先PCA再L1L2
L1:drop_columns(l1):len(4)[‘V34’ ‘V32’ ‘V22’ ‘V15’]
L2:INFO:main:drop_columns(l1):len(3)[‘V6_pca’ ‘V13’ ‘V21’]
remain feature_columns:len(30)[‘V36_pca’ ‘V8’ ‘V5’ ‘V7_pca’ ‘V37’ ‘V29’ ‘V24’ ‘V25’ ‘V31’ ‘V35’ ‘V28’
‘V30’ ‘V20’ ‘V23’ ‘V18’ ‘V33’ ‘V26’ ‘V19’ ‘V4’ ‘V9’ ‘V14’ ‘V10_pca’ ‘V11’
‘V17’ ‘V12’ ‘V3’ ‘V2’ ‘V1’ ‘V0’ ‘V27’]
可见:L1后效果较好,L2后效果不佳,但LR,SVR,经过L2提高了。
所以暂时不执行L2流程。保留特征
先L1,L2在PCA
PCA之后,剩余特征按最初思路执行,移除特征(等价于先执行L1,L2再执行PCA)
[‘V31’ ‘V15’ ‘V21’]
[‘V32’ ‘V13’ ‘V34’]
哼上面相比可以发现,差异在于,V6_pca,V15,V22的处理上
可见,结果依然不如最初先PCA,在L1,L2
采用先PCA,再L1,不执行L2
最终效果(第一个score_df)
6,特征处理04_特征运算(maxmin归一化,高相关性特征)
先maxmin归一化到(1,2)区间
四则运算,[v0,v1],[v1,v8],[v8,v27]等均发现 乘法or 加法的mic提升,但实际对算法基本没提升
怀疑是特殊有特殊的分布规律导致。
高相关pair:[(‘V0’, ‘V1’), (‘V1’, ‘V8’), (‘V8’, ‘V27’), (‘V8’, ‘V31’)]
前三个:(‘V0’, ‘V1’), (‘V1’, ‘V8’), (‘V8’, ‘V27’)
只有:V0_V1_multi作为新特征不错(需结合V0,V1原始特征)
由于不大具有普适性,所以暂不采用。
TODO 观察数据分布特征
7,特证处理05_基于方差的特征筛选
参考;10_特证处理05_基于方差的特征筛选.txt
方差阈值:0.75
INFO:main:drop_columns:len(7)[‘V11’ ‘V17’ ‘V20’ ‘V21’ ‘V22’ ‘V27’ ‘V5’]
方差阈值:0.70
INFO:main:drop_columns:len(6)[‘V17’ ‘V20’ ‘V21’ ‘V22’ ‘V27’ ‘V5’]
8,特征处理06_RFECV特征筛选
参考:11_特征处理06_RFECV特征筛选.txt
LinearSVR和LinearRegression特征筛选都不错,按照多保留原则采用LinearSVR的方式,丢弃1个特征
结合特征处理03,
结合特征处理03,之后进行rfecv筛选。
[‘V0’, ‘V1’, ‘V2’, ‘V3’, ‘V4’, ‘V5’, ‘V8’, ‘V9’, ‘V11’, ‘V12’,’V13’, ‘V14’, ‘V17’, ‘V18’, ‘V19’, ‘V20’, ‘V21’, ‘V23’, ‘V24’, ‘V25’,’V26’, ‘V27’, ‘V28’, ‘V29’, ‘V30’, ‘V31’, ‘V33’, ‘V35’, ‘V37’, ‘V6_pca’,’V7_pca’, ‘V10_pca’, ‘V36_pca’]
INFO:root:model_name:XGBRegressor
INFO:main:有效特征个数 : 27
INFO:root:model_name:RandomForestRegressor
INFO:main:有效特征个数 : 14
INFO:root:model_name:LinearSVR
INFO:main:有效特征个数 : 23
INFO:root:model_name:LinearRegression
INFO:main:有效特征个数 : 23
结论:效果略微提升
9,特征处理07_特征log正态化(其他算法尝试)
参考:12_特征处理07_特征log正态化(其他算法尝试).txt
先尝试分布相关模型,其他模型:BayesianRidge,GaussianProcessRegressor,ElasticNetCV
通过观察,V1,V31左右sum对称,可转为正态分布
以下分别V1,处理前后,V31处理前后。
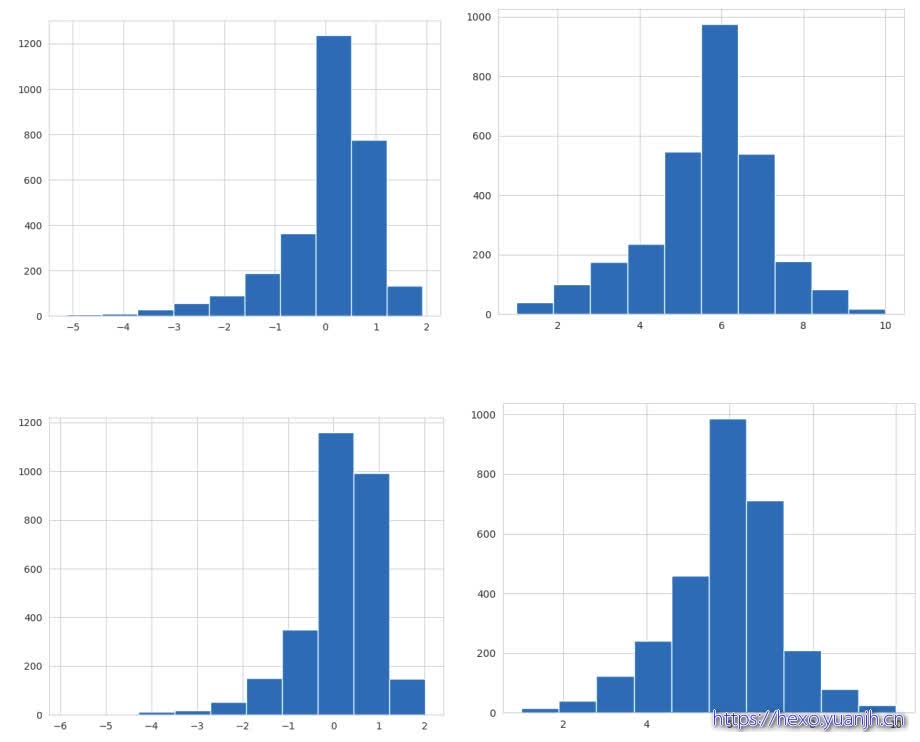
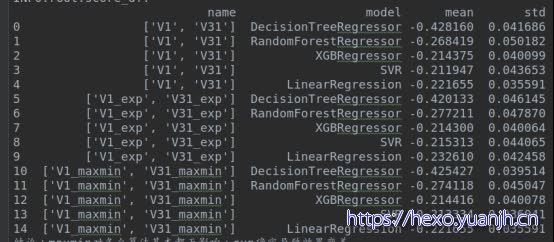
结论:最终效果变差,怀疑原因,target非正态分布导致,因子正态时可能不合适(不在同分布)
尝试将target转为正态分布
以下分别为原始target,target(np.log(maxmin(1,2))),target(np.log(maxmin(1,1.5)))(np.log(maxmin(0,1))报错)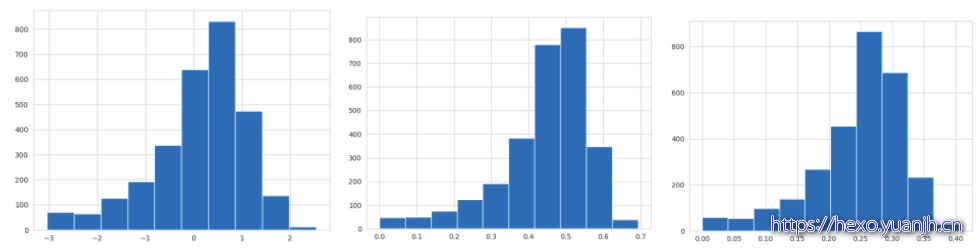
,np.sqrt(maxmin(0,1)),np.sqrt(maxmin(1,2)),np.exp(maxmin(0,1)),np.exp(maxmin(1,2)),
np.square(maxmin(0,1)),Np.square(maxmin(1,2))
使用V1和V31得到的假正态分布,v1_exp,v31_exp和target转化的正态分布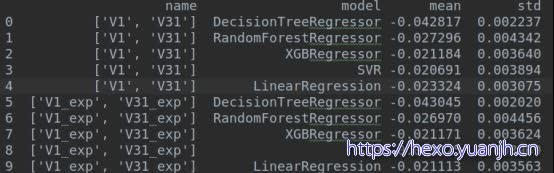
结论:基本无影响,lr优化,svr变差
10,特征处理08_maxmin及多项式回归
在使用pca和l1丢弃特征的情况下测试(减少无用特征干扰,多项式时特征膨胀)
1,多项式回归使用钱先maxmin到(0,1)。避免乘法产生同号异号带来的不搭调的拐点
2,归一化到(1,2),避免乘法导致的单调性丧失
3,特征采用L1,L2筛选,避免特征爆炸
最终最优为L1后的特征
4,测试仅maxmin归一化的效果
Maxmin(0,1),maxmin(1,2)基本完全一致
结论:同上面的多项式扩展比较,多项式扩展确实微弱提升效果。(svr,rfr)
11,特征处理09_首尾异常点清理及和pcaL1Maxmin的结合
参考:14_特征处理09_首尾异常点清理及和pcaL1Maxmin的结合.txt
结论:特征[‘V0’, ‘V1’, ‘V8’, ‘V27’, ‘V31’]采用01234的方式会有提升(主要是LR)
剩下的第二批特征,会导致效果变差
采用01234方式,[‘V0’, ‘V1’, ‘V8’, ‘V27’, ‘V31’]的效果提升
结合PCA,L1综合效果
结合maxmin(0,1)的效果
12,特征处理10_参考特征正态化
参考:16_特征处理10_参考特征正态化.txt
V0,1,6,Exp(maxmin())
V30:log(maxmin()))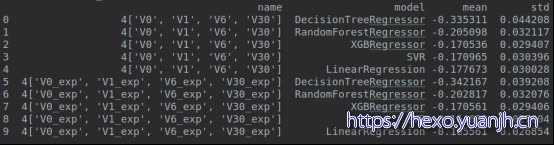
LR上弱提升
参考另一篇文章的自动化正态化模型(Boxcox)
仅特征正态化,target不处理则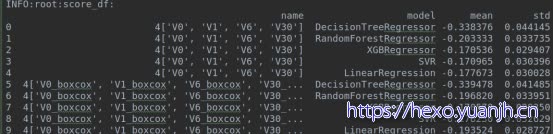
可见:基本更差,svr,和lr弱差,其他不变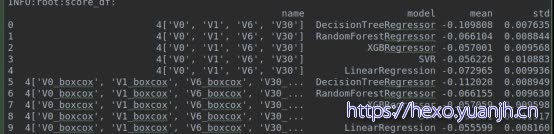
可见:LR有较显著的降低,其他基本不变。
参考文章思路,对所有特征全部正态化转化
将ori target tmp_df1 的上半部分和boxcox target boxcox scoring tmp_df1:的下半部分比对
可见,误差其实变大了,也就是说boxcox并未对结果提升
13,特征处理11_参考_丢弃不同分布特征
他人结论:’V5’, ‘V17’, ‘V28’, ‘V22’, ‘V11’, ‘V9’
特殊列:
平移偏移:V2,v6,v11,v13,v14,v16,v37
不一致分布:V5,v9,v17,v19,v20,v21,v27,v35
缺口分布:V3,v7,v32
在执行PCA,L1过滤后丢弃这6列,
结论:丢弃对结果有微弱影响,LR影响最大,下降0.005点。
14,特征处理12_参考_丢弃脏数据
参考:19_特征处理12_参考_丢弃脏数据.txt
参考内容:工业蒸汽模型代码分享mse=0.095
https://tianchi.aliyun.com/notebook/detail.html?spm=5176.11409386.0.0.32f81d07uxLsiA&id=41563
采用基于算法的异常点清除方式,算法预测误差在mean+/- 3*std范围外误差都认为异常数据。
可见SVR筛选后特征最优的。基本在所有算法上都取得最好效果。
不过这些数据都是基于去除异常点后的数据集,可能无法反映完全真实训练集情况。
基础策略01
SVR过滤异常行 ->PCA过滤 ->丢弃L1的4特征 ->丢弃不同分布6特征(实际5)
效果:
基础策略01_改造01
将基准策略中特征丢弃,放到一开始就执行,丢弃特征,在丢弃行
也就是按照3,4,1,2重新组装
效果:
15,特征处理13_多处理方式结合
基础策略01_改造01_改造01
流程初始阶段添加maxmin(0,1)
基础策略02,各步骤重走
初始->L1(drop3)->L2(drop3)->PCA->SVR行过滤
继续->丢弃6不同分布的特征
基础策略02_改造01
初始之前添加对所有feature的maxmin归一化(0,1)
归一化(svr比未归一提高)->L1(drop8)->L2(drop0)->PCA(V16不存在,故关闭)->SVR行过滤
效果:
另分支
归一化(svr比未归一提高)->L1(drop8,特殊处理保留V16)->L2(drop0)->PCA->SVR行过滤
效果:
继续执行步骤,丢弃分布不一致的特征列
16,特征处理14_列边缘点清理
清理前打分,清理后比较,并没什么效果
尝试:0.025,0.975
和0.001,0.999
均无用
17,特征处理15_maxmin和分位切首尾结合
参考:22_特征处理15_maxmin和分位切首尾结合.txt
先分位切分在maxmin(0,1)
和直接maxmin(0,1)比对
结论:添加分位处理后结果变差,所以不使用.
18,算法调参
特征工程部分就按照
15_特征处理13_多处理方式结合里面的
基础策略01_改造01_改造01
参考思路
B,部分是类别属性,不是离散值
3,0.12是可以用单模型跑出来的,特征工程和模型要选对,这个问题训练集少很容易过拟合。0.11的成绩我目前是做了bagging的模型融合跑出来的。
5,其他automl工具尝试
最终成绩(TOP4.7%,121/2575)
2020.02:这个项目又开放提交了,目前排名400/4795,8.3%的样子.排名果然下降很多.由于项目是带奖金项目,获奖者需要公开分享预测思路,一旦思路公开,可以对成绩有较大提升.
参考文章
1,工业蒸汽模型代码分享mse=0.095
Url:https://tianchi.aliyun.com/notebook/detail.html?spm=5176.11409386.0.0.616c1d079RBnBY&id=41563
借鉴点:
a.丢弃不同分布特征
b.错误位于mean+-3std的数据认为异常点,丢弃
c.数据拆分为train,valid,test三部分
d.Np.power形式将target转为正态分布形似
e.所有特征都进行自动化正态化处理
相关疑问和语句
(程序和自己所想是否一致)
FeatureToolsReg.get_columns_pic(train_data_tmp, target_column=’V0_dummy_split_(1.153, 2.121]’,feature_column_list=[‘V0’])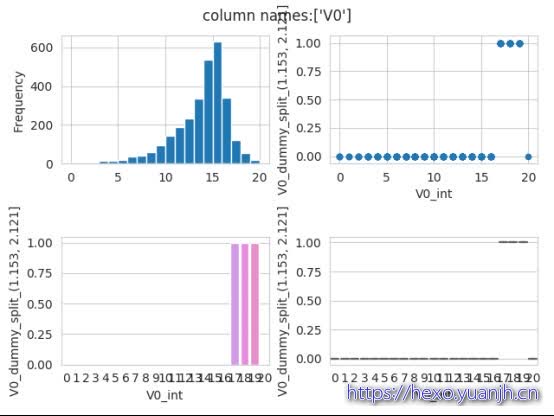
验证掐头去尾正确性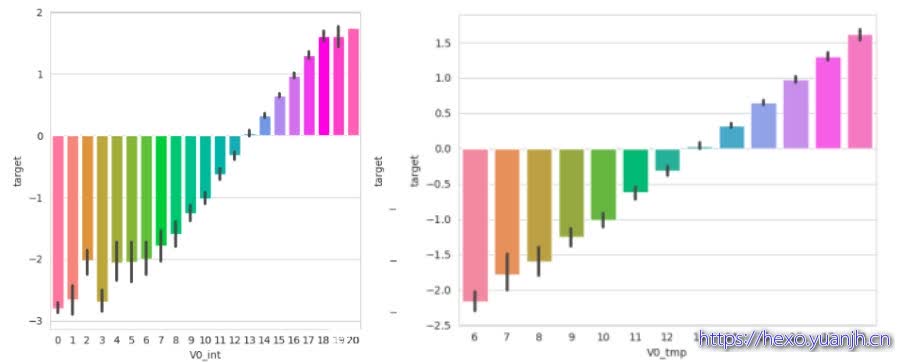
1 | #绘制原始图形 |
误差分析
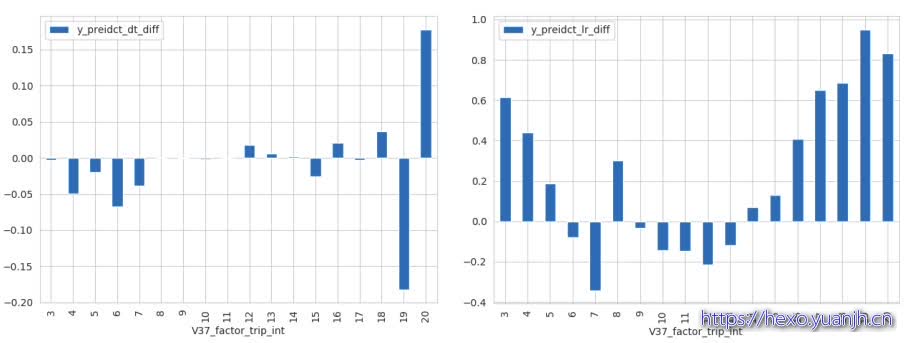
分别为dt,lr的分布和误差图(第一行分布,第二行误差)
个人步骤整理
1,特征概况,容易objt-》int的先处理掉,转为好处理的特征
TODO交叉特征处理
TODO 不同的特征组采用不同算法