简单复习,整理下神经网络相关知识点
什么是卷积神经网络
卷积神经网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。它的特殊性体现在两个方面,一方面它的神经元间的连接是非全连接的(局部感受野), 另一方面同一层中某些神经元之间的连接的权重是相同的(权值共享)。局部感受野和权值共享这两大神器使CNN更类似于生物神经网络,降低了网络模型的复杂度,减少了权值的数量。
1)卷积神经网络是一种前馈神经网络,前面讲的网络包括full NN,感知器都是前馈网络,BP是一种前馈网络的训练方法。
2) 卷积神经网络主要是降维,有点类似PBA
CNN的基本结构包括两层,其一为特征提取层,每个神经元的输入与前一层的局部接受域相连,并提取该局部的特征。一旦该局部特征被提取后,它与其它特征间的位置关系也随之确定下来;其二是特征映射层,网络的每个计算层由多个特征映射组成,每个特征映射是一个平面,平面上所有神经元的权值相等。特征映射结构采用影响函数核小的sigmoid函数作为卷积网络的激活函数,使得特征映射具有位移不变性
主要组成
卷积层(Convolutional layer),卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征。
池化层(Pooling),它实际上一种形式的向下采样。有多种不同形式的非线性池化函数,而其中最大池化(Max pooling)和平均采样是最为常见的
全连接层(Full connection), 与普通神经网络一样的连接方式,一般都在最后几层
pooling层的作用:
Pooling层相当于把一张分辨率较高的图片转化为分辨率较低的图片;
pooling层可进一步缩小最后全连接层中节点的个数,从而达到减少整个神经网络中参数的目的。
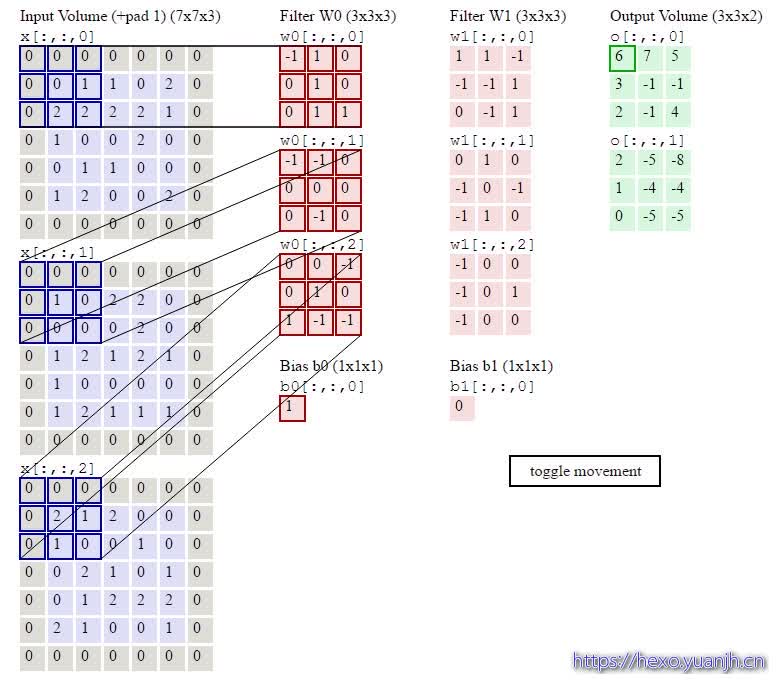
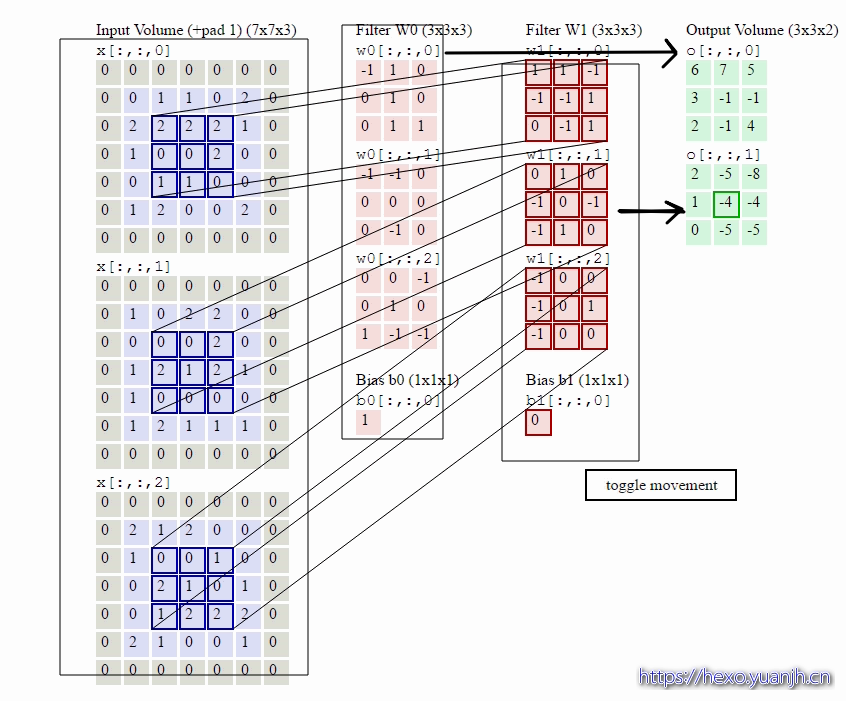
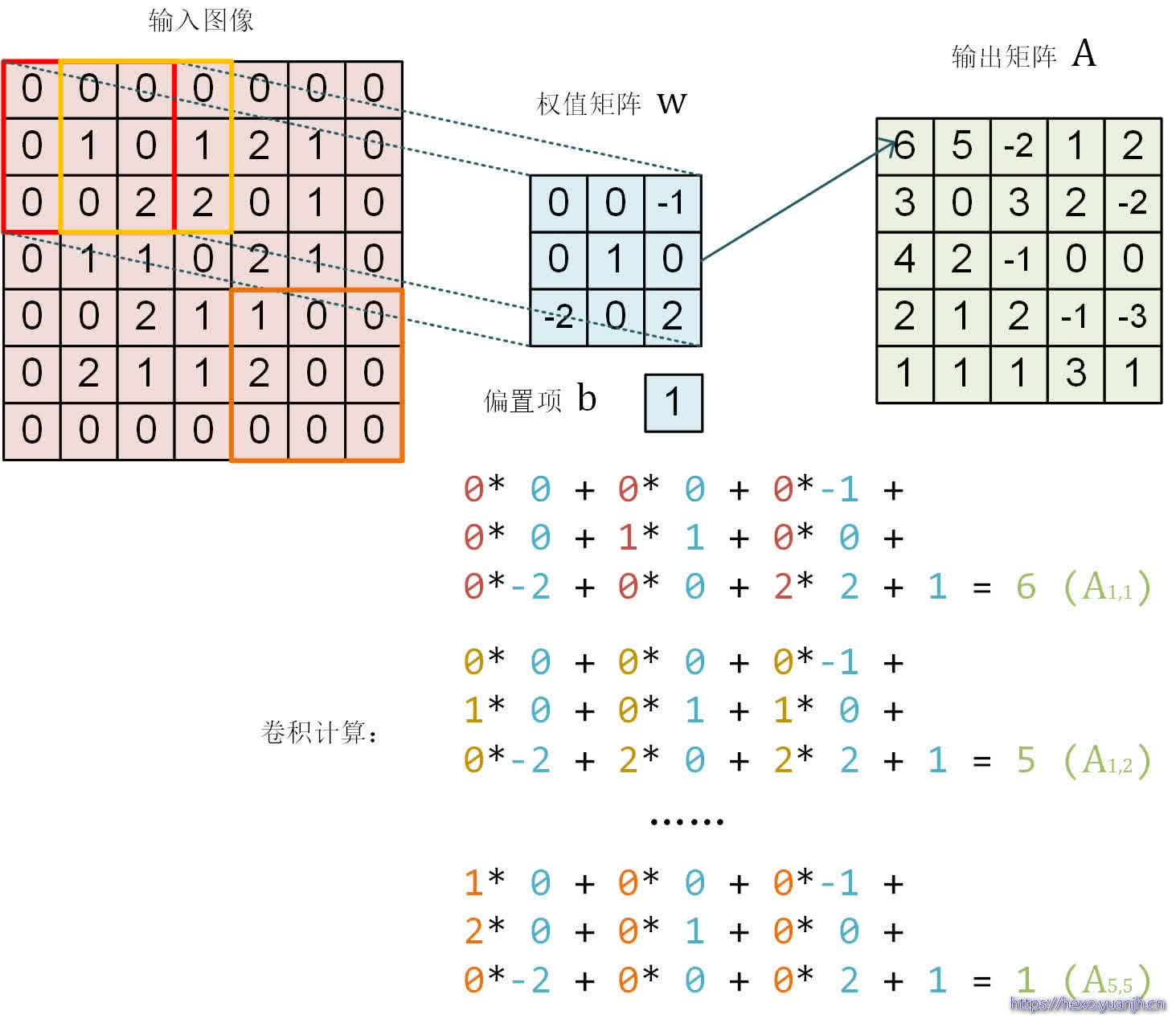
卷积的计算
本人更倾向于将卷积看做“积卷”,因为其是先做积(乘法),在做卷(加法)
网上找了几个动图,可以比较清晰的展示这个过程
动图地址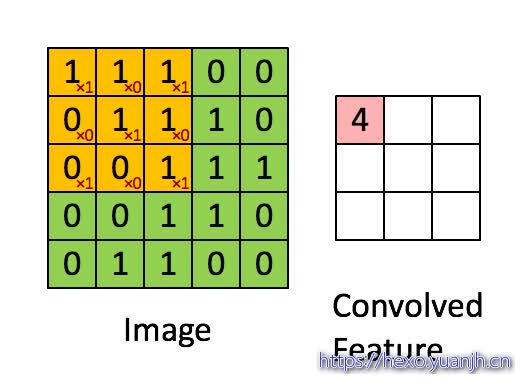
这里面体现了局部连接和权值共享:每层神经元只和上一层部分神经元相连(卷积计算规则),且filter的权值对于上一层所有神经元都是一样的。对于包含两个333的fitler的卷积层来说,其参数数量仅有(333+1)*2=56个,且参数数量与上一层神经元个数无关。与全连接神经网络相比,其参数数量大大减少了。
卷积运算一个重要的特点就是,通过卷积运算,可以使原信号特征增强,并且降低噪音
Pooling层输出值的计算
Pooling层主要的作用是下采样,通过去掉Feature Map中不重要的样本,进一步减少参数数量。Pooling的方法很多,最常用的是Max Pooling。Max Pooling实际上就是在nn的样本中取最大值,作为采样后的样本值。下图是2\2 max pooling: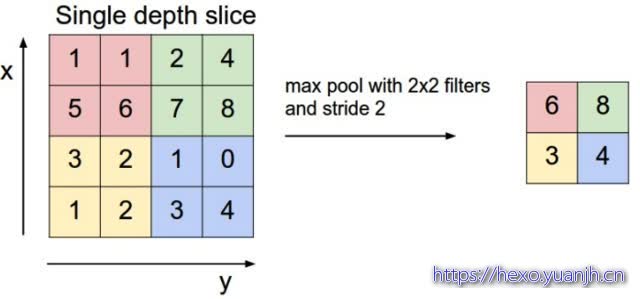
除了Max Pooing之外,常用的还有Mean Pooling——取各样本的平均值。
对于深度为D的Feature Map,各层独立做Pooling,因此Pooling后的深度仍然为D。
为什么是下采样?利用图像局部相关性的原理,对图像进行子抽样,可以减少数据处理量同时保留有用信息
池化层通常接在卷积层后面。池化这个词听着就很有学问,其实引入它的目的就是为了简化卷积层的输出。通俗地理解,池化层也在卷积层上架了一个窗口,但这个窗口比卷积层的窗口简单许多,不需要w,b这些参数,它只是对窗口范围内的神经元做简单的操作,如求和,求最大值,把求得的值作为池化层神经元的输入值。
max-pooling做的事就是去检测这个特征是否在窗口覆盖范围的区域内。这也导致了,它会丢失这种特征所在的精准位置信息,所幸的是池化层可以保留相对位置信息。而后者相比而言比前者更重要。
max-pooling技术只是池化技术的一种,还有一种比较常用的是L2-pooling,与max-pooling唯一的区别就是在池化窗口扫过的区域里做的操作不是求最大值,而是所有神经元平方后求和再开根号,这和我们L2正则对权值参数的操作是一样的。实际操作中,这两种方式都是比较常用的。池化操作方式的选择也是我们调参工作的一部分,我们可以根据validation data集来调节,选择更好的池化操作。
LeNet-5(识别数字的卷积网络)
LenNet-5共有7层(不包括输入层),每层都包含不同数量的训练参数,如下图所示。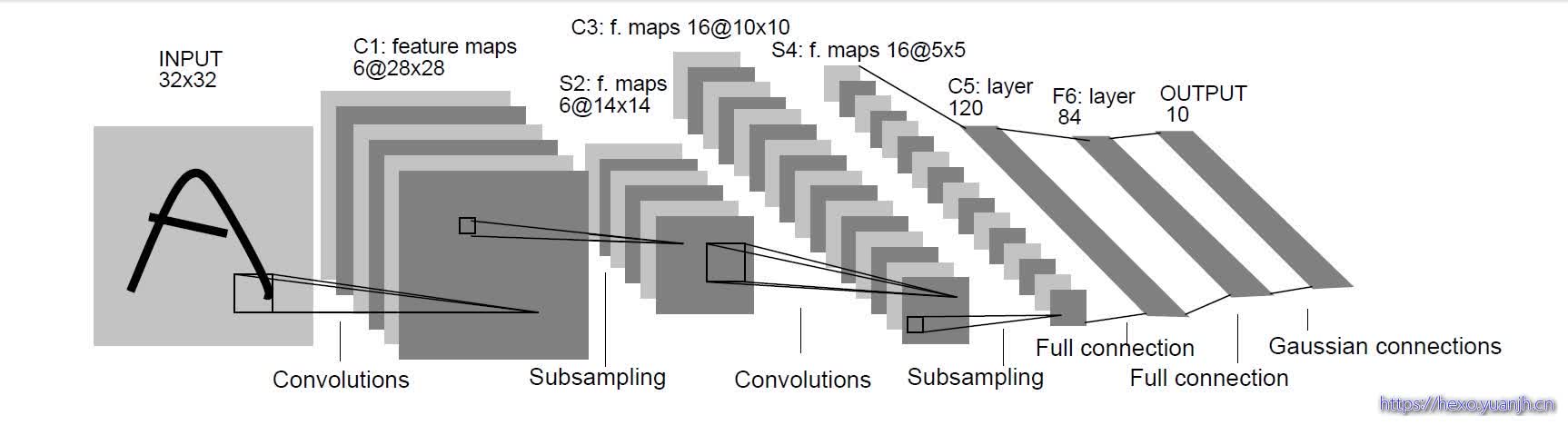
特殊留意:区分哪些是C,哪些是S,哪些是全连接,哪些是“C,S,全连接”的结果
LeNet-5中主要有2个卷积层、2个下抽样层(池化层)、3个全连接层3种连接方式
卷积层
卷积层采用的都是5x5大小的卷积核/过滤器(kernel/filter),且卷积核每次滑动一个像素(stride=1),一个特征图谱使用同一个卷积核.
每个上层节点的值乘以连接上的参数,把这些乘积及一个偏置参数相加得到一个和,把该和输入激活函数,激活函数的输出即是下一层节点的值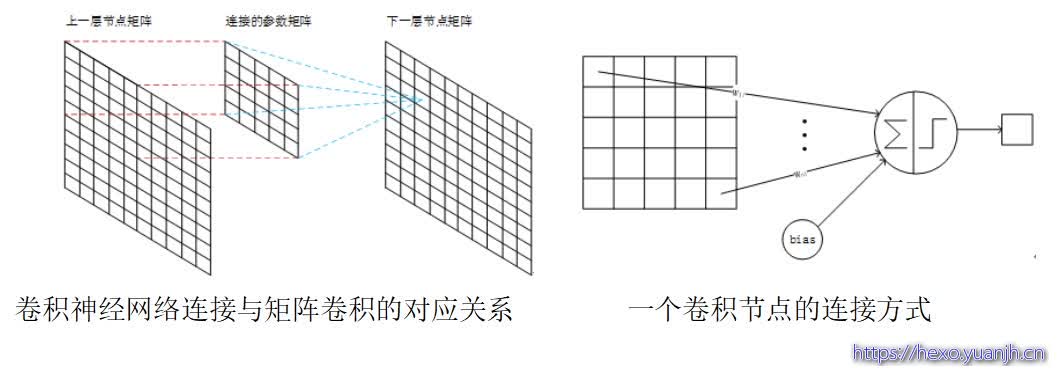
LeNet-5的下采样层(pooling层)
下抽样层采用的是2x2的输入域,即上一层的4个节点作为下一层1个节点的输入,且输入域不重叠,即每次滑动2个像素,下抽样节点的结构如下: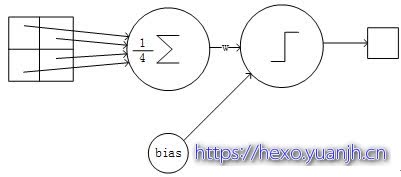
每个下抽样节点的4个输入节点求和后取平均(平均池化),均值乘以一个参数加上一个偏置参数作为激活函数的输入,激活函数的输出即是下一层节点的值。
卷积后输出层矩阵宽度的计算:
1 | Outlength=(inlength-fileterlength+2*padding)/stridelength+1 |
LeNet-5第一层:卷积层C1
C1层是卷积层,形成6个特征图谱。卷积的输入区域大小是5x5,每个特征图谱内参数共享,即每个特征图谱内只使用一个共同卷积核,卷积核有5x5个连接参数加上1个偏置共26个参数。卷积区域每次滑动一个像素,这样卷积层形成的每个特征图谱大小是(32-5)/1+1=28x28。C1层共有26x6=156个训练参数,有(5x5+1)x28x28x6=122304个连接。
LeNet-5第二层:池化层S2
S2层是一个下采样层(为什么是下采样?利用图像局部相关性的原理,对图像进行子抽样,可以减少数据处理量同时保留有用信息)。C1层的6个28x28的特征图谱分别进行以2x2为单位的下抽样得到6个14x14((28-2)/2+1)的图。每个特征图谱使用一个下抽样核。5x14x14x6=5880个连接。
LeNet-5第三层:卷积层C3
C3层是一个卷积层,卷积和和C1相同,不同的是C3的每个节点与S2中的多个图相连。C3层有16个10x10(14-5+1)的图,每个图与S2层的连接的方式如下表 所示。C3与S2中前3个图相连的卷积结构见下图.这种不对称的组合连接的方式有利于提取多种组合特征。该层有(5x5x3+1)x6 + (5x5x4 + 1) x 3 + (5x5x4 +1)x6 + (5x5x6+1)x1 = 1516个训练参数,共有1516x10x10=151600个连接。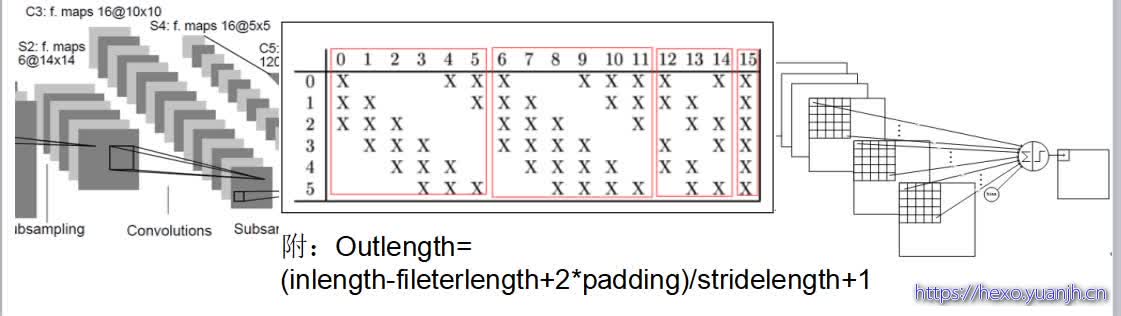
LeNet-5第四层:池化层S4
S4是一个下采样层。C3层的16个10x10的图分别进行以2x2为单位的下抽样得到16个5x5的图。5x5x5x16=2000个连接。连接的方式与S2层类似,如下所示。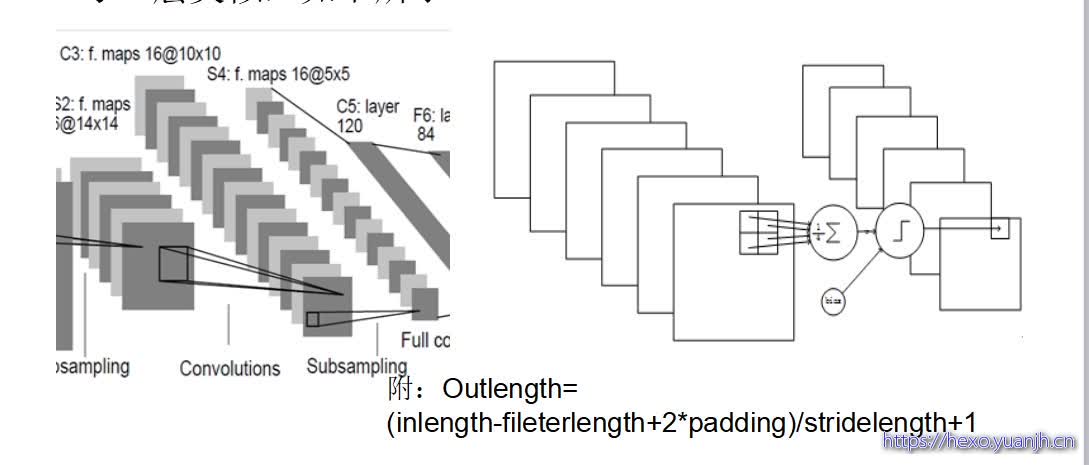
LeNet-5第五层:全连接层C5
C5层是一个全连接层。由于S4层的16个图的大小为5x5,与卷积核的大小相同,所以卷积后形成的图的大小为1x1。这里形成120个卷积结果。每个都与上一层的16个图相连。所以共有(5x5x16+1)x120 = 48120个参数,同样有48120个连接。C5层的网络结构如下所示。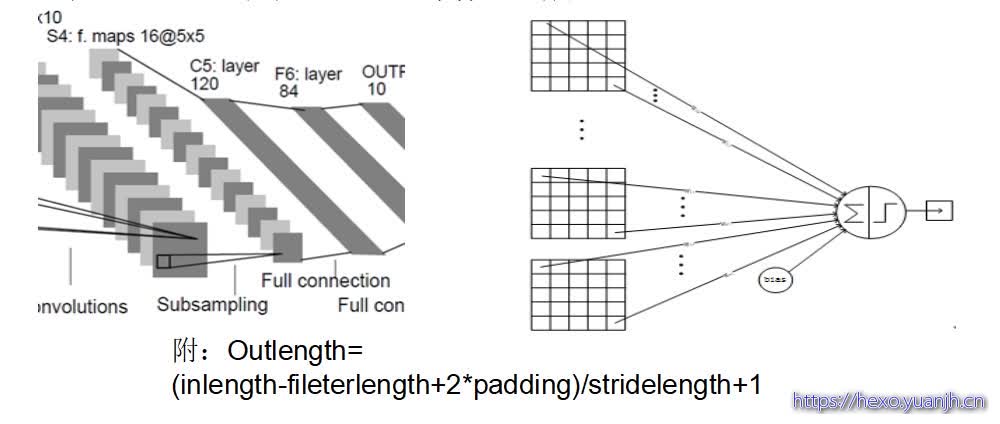
LeNet-5第六层:全连接层F6
F6层是全连接层。F6层有84个节点,对应于一个7x12的比特图,该层的训练参数和连接数都是(120 + 1)x84=10164.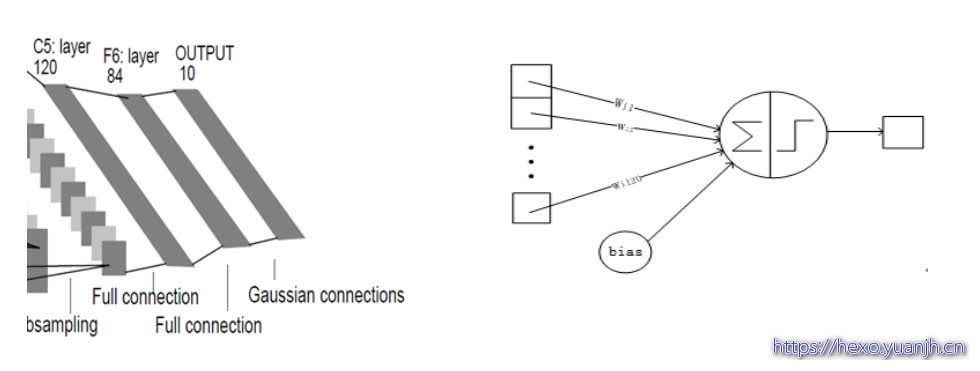
LeNet-5第七层:全连接层Output
Output层也是全连接层,共有10个节点,分别代表数字0到9,如果节点i的输出值为0,则网络识别的结果是数字i。采用的是径向基函数(RBF)的网络连接方式。假设x是上一层的输入,y是RBF的输出,则RBF输出的计算方式是: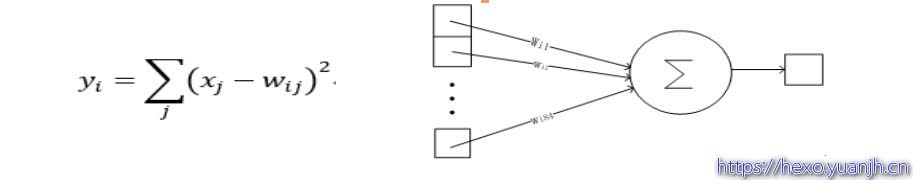
yi的值由i的比特图编码(即参数Wij)确定。yi越接近于0,则标明输入越接近于i的比特图编码,表示当前网络输入的识别结果是字符i。该层有84x10=840个设定的参数和连接。连接的方式如上图.
以上是LeNet-5的卷积神经网络的完整结构,共约有60,840个训练参数,340,908个连接。
简化的LeNet-5系统
参考:Deep Learning模型之:CNN卷积神经网络(二) 文字识别系统LeNet-5:https://blog.csdn.net/u010555688/article/details/24848367
常见问题
常用激活函数
Sigmoid:将数据映射到0-1范围内
Tanh:将数据映射到-1-1的范围内
ReLU:小于0的值就变成0,大于0的等于它本身
注:常用ReLU作为激活函数而不用simgoid和tanh作为激活函数的原因是:加速收敛。因为sigmoid和tanh都是饱和(saturating)的。何为饱和?把这两者的函数曲线和导数曲线plot出来就知道了:他们的导数都是倒过来的碗状,也就是,越接近目标,对应的导数越小。而ReLu的导数对于大于0的部分恒为1。于是ReLU确实可以在BP的时候能够将梯度很好地传到较前面的网络。
Softmax回归
Softmax回归模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签 y 可以取两个以上的值。softmax把一个k维的向量(z1,z2,z3,z4….)映射成一个(σ1,σ2,σ3,σ4….)其中σi是一个0-1的常数,然后可以根据bi的大小来进行多分类的任务,如取权重最大的一维。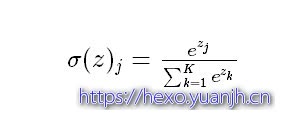
Dropout的作用
训练神经网络模型时,如果训练样本较少,为了防止模型过拟合,Dropout可以作为一种手段供选择。Dropout是hintion最近2年提出的,源于其文章Improving neural networks by preventing co-adaptation of feature detectors.中文大意为:通过阻止特征检测器的共同作用来提高神经网络的性能。说白了就是指在模型训练时随机让网络某些隐含层节点的权重不工作,不工作的那些节点可以暂时认为不是网络结构的一部分,但是它的权重得保留下来(只是暂时不更新而已),下次样本输入时它可能又得工作了。
一般神经网络VS卷积神经网络
相同点:卷积神经网络也使用一种反向传播算法(BP)来进行训练
不同点:网络结构不同。卷积神经网络的网络连接具有局部连接、参数共享的特点。
局部连接:是相对于普通神经网络的全连接而言的,是指这一层的某个节点只与上一层的部分节点相连。
参数共享:是指一层中多个节点的连接共享相同的一组参数。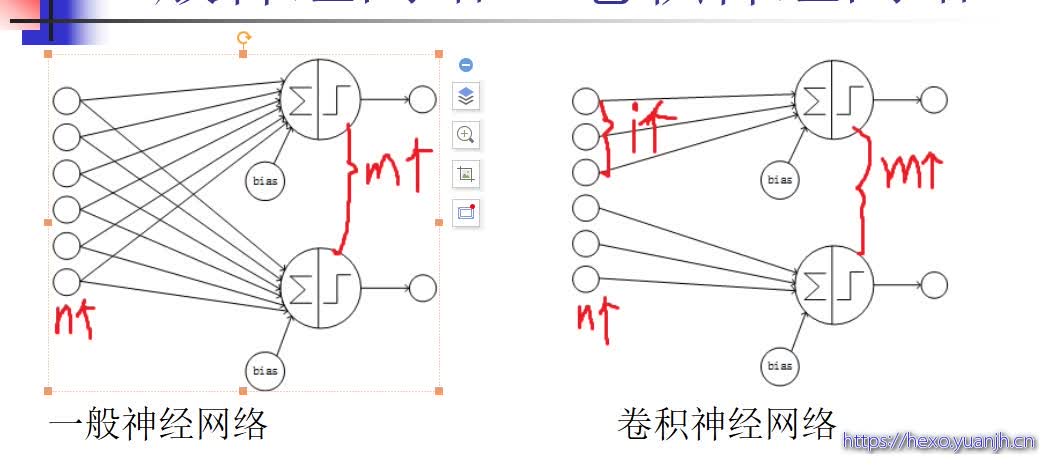
参考
深度学习笔记(六) cnn 卷积神经网络:https://blog.csdn.net/chenfenggang/article/details/77825901?utm_source=blogkpcl13
卷积神经网络(CNN):https://blog.csdn.net/wangchao7281/article/details/72901592
深度学习 CNN卷积神经网络 LeNet-5详解:https://blog.csdn.net/happyorg/article/details/78274066
Deep Learning模型之:CNN卷积神经网络(二) 文字识别系统LeNet-5:https://blog.csdn.net/u010555688/article/details/24848367